Introducción
El presente trabajo aporta una descripción de datos de vivienda para la ciudad de Montevideo e implementa un enfoque de aprendizaje estadístico al desafío de predicción de un activo de difícil valuación como los inmuebles. En primer lugar, se recopilan datos de un sitio web y de registros administrativos de la Dirección General de Registros (DGR) y Dirección Nacional de Catastro (DNC). En segundo lugar, se modela el precio de los inmuebles con técnicas de aprendizaje estadístico, de creciente aplicación en la literatura estadística, computacional e incipientemente económica. Los modelos que se comparan son el modelo lineal, el árbol de regresión y los Bosques aleatorios.
Antecedentes
Los antecedentes relevantes se pueden dividir entre los estudios que tratan sobre el mercado de vivienda en Uruguay y los que aplican técnicas de aprendizaje estadístico para la predicción de precios de vivienda. Para este último punto se encontró un solo trabajo nacional (Goyeneche et al. (2017)) y numerosas referencias internacionales, como la de Čeh et al. (2018).
Dentro de la segunda categoría, se destaca el trabajo de Mullainathan y Spiess (2017), que realiza una introducción a los modelos de aprendizaje estadístico mediante un ejemplo con datos de vivienda. Este artículo, al igual que los de Athey (2018) y Varian (2014) fueron la principal motivación para este trabajo y resultan referencias básicas en la utilización de modelos de aprendizaje estadístico en Economía.
Metodología
Los diversos modelos de aprendizaje estadístico se pueden encontrar resumidos en dos referencias básicas: Friedman et al. (2001) y James et al. (2013). Uno de los modelos que más aparece en la literatura y que se utilizan aquí son los árboles de regresión y clasificación (CART por sus siglas en inglés) y su agregación en bosques aleatorios (random forests).
Además de los modelos anteriormente mencionados, se utiliza un modelo lineal hedónico. Éste fue originalmente introducido por Griliches (1961) para el precio de los automóviles y luego fue desarrollado teórica y conceptualmente por Rosen (1974). Los modelos de precios hedónicos plantean que el precio de un bien puede ser determinado en función de sus características observables. Éstas tienen un precio implícito, el cual puede ser aproximado mediante los coeficientes de un modelo de regresión. En el caso de las viviendas, se trata de bienes heterogéneos compuestos por diferentes características cuya valoración marginal puede ser derivada mediante estos modelos.
Usualmente, en los trabajos empíricos en Econometría y Economía, primero se especifica un modelo, se lo estima en toda la base de datos y se confía en la teoría estadística para obtener intervalos de confianza para los parámetros estimados. De esta forma, el foco está en los efectos estimados del modelo más que en el poder predictivo del mismo (Athey, 2018). Por lo tanto, se pueden tomar a los métodos de aprendizaje estadístico, donde el foco está en la predicción a partir de ejercicios empíricos, como complementarios a lo que se denomina Econometría clásica. En este trabajo, se utilizan arboles de regresión y clasificación (CART), un método de aprendizaje estadístico introducido por Breiman et al. (1984). El principio general de este método es particionar recursivamente el espacio de variables explicativas (que llamaremos predictores) de forma binaria y así determinar subparticiones óptimas para la predicción. Este método tiene la virtud de ser de fácil interpretación, comunicación y transparente. Sin embargo, en la mayoría de los casos tiene peor performance predictiva que un modelo lineal y una serie de falencias asociadas a la estabilidad de las predicciones (Genuer y Poggi, 2017). Esto se puede resolver en gran medida con el método agregativo de bosques aleatorios. Éste es más reciente (Breiman, 2001) y conceptualmente implica una agregación de muchos árboles donde se toma la media de las predicciones individuales como criterio de partición.
Con el fin de comparar los tres modelos, se delimita el trabajo al departamento de Montevideo, por ser el área geográfica de mayor cantidad de datos y, en el caso de los datos de transacciones, mayor confiabilidad de los datos de catastro (Landaberry y Tubio, 2015). La estrategia de comparación elegida consiste en considerar pocos predictores en ambas bases de datos. La modelización se realiza en cada base de datos separadamente (ofertas y transacciones) y por tipo de propiedad (apartamentos y casas).
Para comparar modelos, se toma en cuenta la raíz del error cuadrático medio (RECM) y el error porcentual absoluto medio (EPAM), ambas medidas son tomadas en una muestra de testeo no utilizada para “entrenar” cada modelo.
Datos
Los datos de ofertas fueron recopilados a través de la API (interfaz para acceder a una página web) puesta a disposición por mercadolibre.com. Para ello se utilizó un programa elaborado en Python, utilizando la biblioteca Beautiful Soup (Richardson, 2007). La muestra original incluye todas las ofertas de venta de inmuebles para la ciudad de Montevideo para el período febrero 2018 - enero de 2019 inclusive y se ha ido actualizando con bajadas en intervalos de un mes.
Las transacciones de compraventa de vivienda en Montevideo promediaron las 14.000 por año (flujo de compraventas) mientras que las ofertas disponibles en el sitio mercadolibre.com.uy de apartamentos y casas en venta sumaron 80.000 publicaciones únicas para el período febrero 2018 - enero 2019. El 50% de las publicaciones en el sitio web, están disponibles alrededor de 6 meses o menos (mediana), aunque la dispersión es relevante (Figura 1).
Figura 1. Histograma del tiempo en el sitio de cada publicación
(color refiere al momento de bajada)

Fuente: Elaboración propia con datos descargados de la API de mercadolibre.com.uy
Uno de los atributos con los que se cuenta es la ubicación exacta. Éste se define con dos variables, la latitud y la longitud, las cuales permiten, por ejemplo, definir distancias a puntos deseables de la ciudad (costa este, parques, etc.) y, a su vez, pueden sugerir comportamientos espaciales de los precios.
Por otra parte, a partir de árboles de regresión es posible agrupar datos que sugieran áreas en base a precios: zonas “caras" y zonas “baratas" independientemente del barrio. A continuación, se presentan dos figuras con particiones de los precios, en base a árboles de regresión que toman solamente dos predictores geográficos (latitud y longitud) para el precio del metro cuadrado. En cada región, la predicción refiere al precio del metro cuadrado promedio. Como se puede observar, las particiones son similares (cortes en Bulevar Artigas, Avenida Italia, etc.), aunque los precios promedios difieren en su nivel, lo que puede sugerir la existencia de una brecha relevante entre los precios pedidos y los transados (ver comentarios finales).
Figura 2. Particiones con variables geográficas del precio del m2
ofertado en Montevideo.
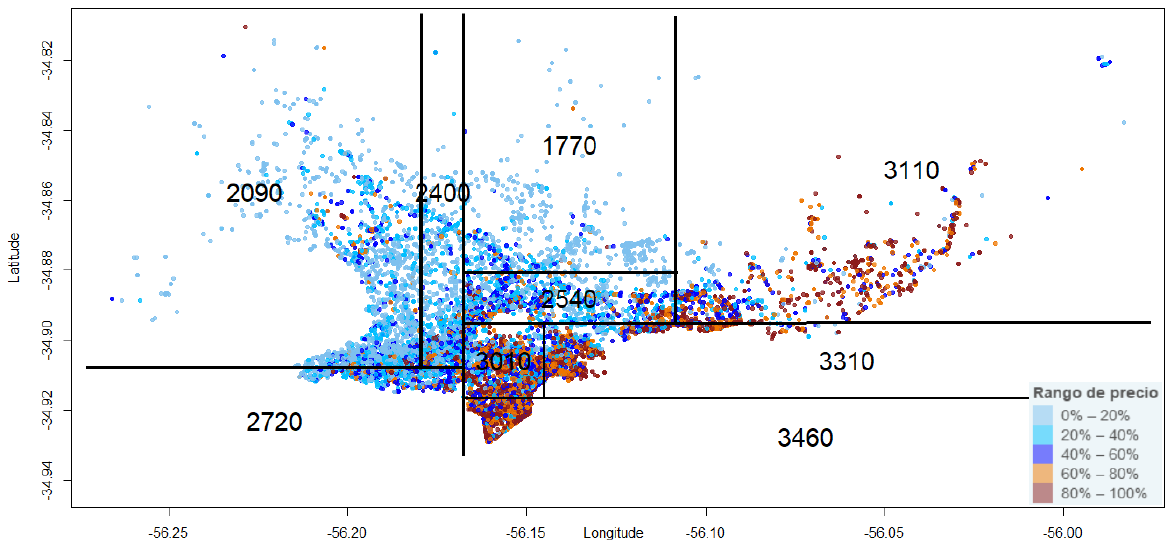
Fuente: Elaboración propia con datos de la API de mercadolibre.com.uy
Figura 3. Particiones con variables geográficas del precio del m2
transado en Montevideo en 2019.
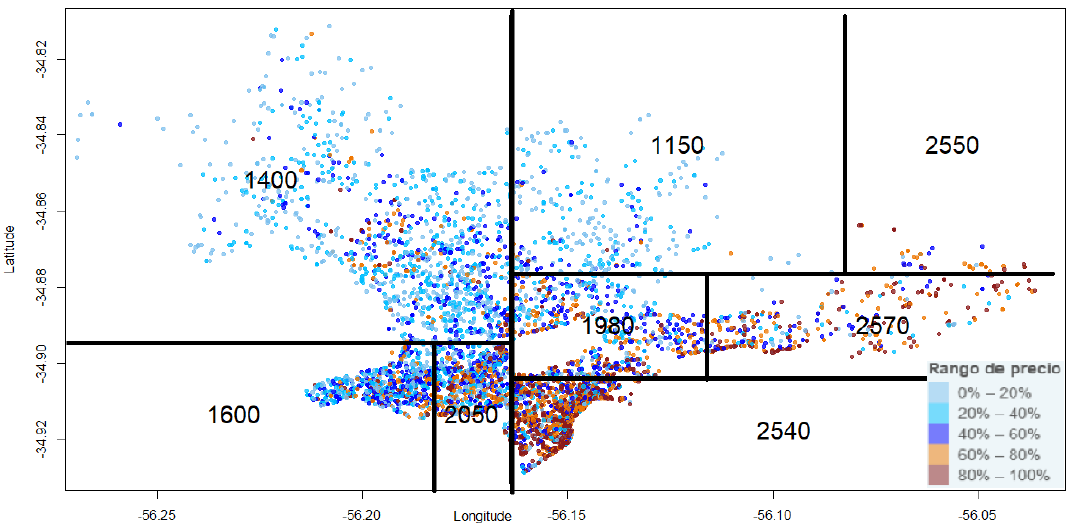
Fuente: Elaboración propia con datos de DGR y DGC.
Resultados
De todos los modelos entrenados, se observan mejoras en la performance predictiva al implementar Bosques aleatorios. Las mejoras relevantes se observan en las bases de datos de ofertas, donde se cuenta con un gran número de observaciones y un grupo confiable de variables. En el caso de las transacciones, tanto la cantidad de observaciones como la menor cantidad de características, pueden influir en los altos errores de predicción.
Tabla 1. Resultados de los modelos para cada base de datos
| Modelos con ofertas - apartamentos | RECM | EPAM |
|---|
| Lineal | USD 47.760 | 17% |
| Árbol | USD 71.420 | 26% |
| Bosque Aleatorio | USD 30.960 | 10% |
| Bosque Aleatorio desarrollado | USD 29.530 | 9% |
| Modelos con ofertas - casas | | |
|---|
| Lineal | USD 75.240 | 22% |
| Árbol | USD 126.740 | 29% |
| Bosque Aleatorio | USD 56.800 | 14% |
| Bosque Aleatorio desarrollado | USD 53.200 | 13% |
| Modelos con transacciones - apartamentos | RECM | EPAM |
|---|
| Lineal | USD 59.030 | 47% |
| Árbol | USD 73.240 | 63% |
| Bosque Aleatorio | USD 52.854 | 44% |
| Bosque Aleatorio desarrollado | USD 50.630 | 42% |
| Modelos con transacciones - casas | | |
|---|
| Lineal | USD 87.050 | 56% |
| Árbol | USD 99.570 | 67% |
| Bosque Aleatorio | USD 86.000 | 56% |
| Bosque Aleatorio desarrollado | USD 76.780 | 50% |
Comentarios finales
Los resultados obtenidos establecen un límite inferior para seguir desarrollando y mejorando los modelos utilizados, por ejemplo, ajustando los parámetros y generando mayor interacción con el componente geográfico. Igualmente, es deseable completar el trabajo contemplando otras técnicas de aprendizaje estadístico y agregaciones. Adicionalmente, los modelos podrían contemplar la dimensión temporal y fundamentos macroeconómicos, aunque el desafío en este caso es mayor y no se existe una literatura extendida.
Por último, la brecha entre el precio pedido y el efectivamente llevado a cabo, puede resultar de interés. Particularmente el estudio de la brecha de precios (oferta vs. transacción) en un contexto como el uruguayo (economía pequeña y dolarizada). Esto puede ser útil para detectar desvíos de fundamentos y establecer una medida de tensión de mercado o indicador adelantado del sector y de la economía. A modo ilustrativo se presenta la evolución en el tiempo del precio del metro cuadrado promedio de apartamentos de menos de 120 metros cuadrados para diferentes zonas. Se puede observar que la diferencia de precios varía según zonas y a través del tiempo.
Referencias
Athey, S., 2018. The Impact of Machine Learning on Economics. In: The Economics of Artificial Intelligence: An Agenda. University of Chicago Press, pp. 1–31.
Breiman, L., 2001. Random forests. Machine learning 45 (1), 5–32.
Breiman, L., Friedman, J., Olshen, R., Stone, C., 1984. Classification and regression trees. Routledge.
Čeh, M., Kilibarda, M., Lisec, A., Bajat, B., 2018. Estimating the performance of random forest vs multiple regression for predicting prices of apartments. International Journal of Geo-Information 7 (5), 168.
Friedman, J., Hastie, T., Tibshirani, R., 2001. The elements of statistical learning. Vol. 1. Springer series in statistics New York.
Genuer, R., Poggi, J.-M., Jan. 2017. Arbres CART et Forêts aléatoires, Importance et sélection de variables.
Goyeneche, J. J., Moreno, L., Scavino, M., 2017. Predicción del valor de un inmueble mediante técnicas agregativas. Serie DT IESTA (17/1).
Griliches, Z., 1961. Hedonic price indexes for automobiles: An econometric of quality change. In: The Price statistics of the federal goverment. NBER, pp. 173–196.
James, G., Witten, D., Hastie, T., Tibshirani, R., 2013. An introduction to statistical learning. Vol. 1. New York: Springer.
Landaberry, V., Tubio, M., 2015. Estimación de ´índice de precios de inmuebles en Uruguay. Documento de trabajo del Banco Central del Uruguay.
Mullainathan, S., Spiess, J., 2017. Machine learning: an applied econometric approach. Journal of Economic Perspectives 31 (2), 87–106.
Richardson, L., 2007. Beautiful soup documentation. Python library.
Rosen, S., 1974. Hedonic prices and implicit markets: product differentiation in pure competition. Journal of political economy 82 (1), 34–55.
Varian, H. R., 2014. Big data: New tricks for econometrics. Journal of Economic Perspectives 28 (2), 3–28.
Documento de trabajo
 | Picardo, P. (2019). Predicción de precios de vivienda. Aprendizaje estadístico con datos de oferta y transacciones para la ciudad de Montevideo.
Documento de trabajo, 002-2019. Banco Central del Uruguay. |
